Rumus JUMLAH n SUKU PERTAMA BARISAN ARITMATIKA
contoh :

2 diambil karena ada 2 buah suku yang qt jumlahkan dan 5 dari rata-ratanya (4+6)/2
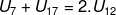
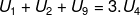
bahkan untuk pemodelan soal yang seperti g masalah dapat qt hitung sebagai
g masalah dapat qt hitung sebagai 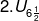
memang secara teori membilang kudu dimulai dengan n Asli tetapi untuk perhitungan
n yang pecahan masih bisa dipakai.
contoh :
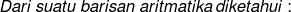
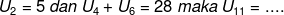
Jawab :
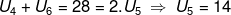
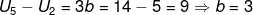

contoh :
Dari suatu barisan aritmatika diketahui :
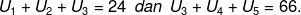
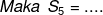
Jawab :
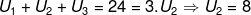
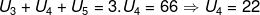
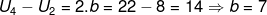
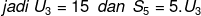
Sehingga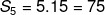
Sekarang perhatikan lagi rumus berikut :
.b%20\right%20\})
Jika qt uraikan akan menjadi
.n^{2}+\left%20(\frac{2a-b}{2}%20\right%20).n)
sehingga dapat qt simpulkan sbb :
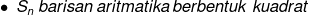
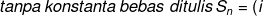.n^{2}+(ii).n)
\:%20koefisien\:%20n^{2}%20\:%20sama-dengan%20\:%20\:%20\frac{beda}{2})
+(ii)\:%20\:%20sama-dengan%20\:%20\:%20suku-awal) .
.
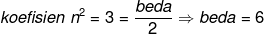
+(-4)=-1=suku%20\:%20awal)
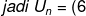n+(-7).....kok\:%20biso\:%20?dipikir\,%20dulu\,%20dunk%20\:%20COY)
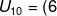.10+(-7)=53)
2 diambil karena ada 2 buah suku yang qt jumlahkan dan 5 dari rata-ratanya (4+6)/2
bahkan untuk pemodelan soal yang seperti
memang secara teori membilang kudu dimulai dengan n Asli tetapi untuk perhitungan
n yang pecahan masih bisa dipakai.
contoh :
Jawab :
contoh :
Dari suatu barisan aritmatika diketahui :
Jawab :
Sehingga
Sekarang perhatikan lagi rumus berikut :
Jika qt uraikan akan menjadi
sehingga dapat qt simpulkan sbb :
JADI UNTUK BARISAN ARITMATIKA PERLU DIINGAT JUMLAH KOEFISIEN DARI SUKU KE-n SAMA DENGAN JUMLAH KOEFISIEN DARI JUMLAH SAMPAI n SUKU YANG PERTAMA YAITU MENGARAH PADA SUKU AWAL
CONTOH :
Dari barisan aritmatika 8,14,20,...........,Un
Tentukan Un dan Sn.
JAWAB
suku awal = 8
beda = 4
separoh beda = 2
jadi Un = 4n + 4 dan 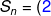.n^{2}+(6).n%20=%202n^{2}+6n)
CONTOH :
Jumlah n suku pertama suatu barisan aritmatika adalah 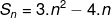
maka nilai suku-10 adalah....
maka nilai suku-10 adalah....
JAWAB
CONTOH :
Diketahui Jumlah 5 suku pertama suatu barisan aritmatika adalah 55 dan
Jumlah 9 suku pertamanya adalah 171 maka nilai suku-2 adalah....
Jumlah 9 suku pertamanya adalah 171 maka nilai suku-2 adalah....
JAWAB


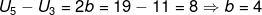
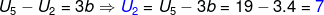
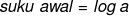
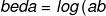-log\,%20a=log\,%20a+log\,%20b-log\,%20a=log\,%20b)
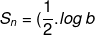n^{2}+(log\,%20a-\frac{1}{2}.log\,%20b).n)
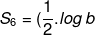6^{2}+(log\,%20a-\frac{1}{2}.log\,%20b).6=18.log\,%20b+6.log\,%20a-3.log\,%20b)

CONTOH :
Diketahui deret aritmatika :
+log\,%20(ab^{2})+log\,%20(ab^{3})+......+U_{n})
Jumlah 6 suku pertamanya adalah ....
Jumlah 6 suku pertamanya adalah ....
JAWAB
CONTOH :
Suku ke-n barisan aritmatika adalah Un = 6n + 4. Disetiap antara 2 sukunya
disisipkan 2 suku baru, sehingga terbentuk barisan aritmatika. Jumlah n suku
pertama deret yang terjadi adalah....
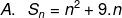
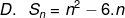
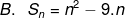
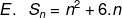
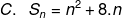
disisipkan 2 suku baru, sehingga terbentuk barisan aritmatika. Jumlah n suku
pertama deret yang terjadi adalah....
JAWAB

Apabila suatu barisan disisipkan diantara 2 sukunya dengan k bilangan yang sama maka posisi yang tidak mengalami perubahan adalah :
SUKU AWAL 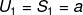
, SUKU TENGAH
& SUKU AKHIR
Jadi Cek pada jawaban , yg mana jika qt masukkan n = 1 hasilnya adalah 10.
nach g ada yg lain khan kecuali A.
kritik n sarannya
BalasHapusaq tunggu sob....thx atas
kunjungan'e