Deret geometri ini disebut juga
DERET GEOMETRI KONVERGEN (mengumpul) atau
DERET GEOMETRI YANG MEMPUNYAI NILAI PENDEKATAN(LIMIT).
Jumlah n suku pertama deret geometri (ukur / kali) adalah :
}{r-1},\: r>1)
untuk menghitung sampai n tak hingganya qt memakai pendekatan (limit) yaitu :
}{1-r}=\frac{a}{1-r}\, ,\, \lim_{n\rightarrow \infty }r^{n}=0\, untuk\, -1<r<1)
untuk rasio yang yang bukan - 1 < r < 1 maka disebut deret geometri yang divergen
(menyebar) dan mempunyai jumlah yang takhingga untuk n yang tak hingga pula.
Contoh :
Jumlah deret geometri tak hingga 6, jika jumlah suku-suku yang bernomor ganjil adalah 4 maka
rumus suku ke - n deret tersebut adalah.....
Jawab :
Jumlah semua sukunya :
) Jumlah semua sukunya yang ber nomor ganjil :
Jumlah semua sukunya yang ber nomor ganjil : Jawab :
+\left ( \frac{b}{a} \right )^{2}+\left ( \frac{b}{a} \right )^{3}+...=\frac{\frac{b}{a}}{1-\frac{b}{a}}=\frac{b}{a-b})
kita cari dulu berapa nilai a dan b nya.

Contoh :
\, maka\, nilai\, 1-p+p^{2}-p^{4}+p^{6}-...=....)
Jawab :
Contoh :
Agar deret :
+\, ^{2}log^{2}(3x-2)+\, ^{2}log^{3}(3x-2)+....)
konvergen maka....
Jawab :
syarat untuk logaritma nya kan belum ea coy....yaitu numerus kudu > 0
Contoh :
Jika r adalah rasio geret geometri dan
^{2}}+\frac{1}{\left (4+r \right )^{3}}+...)
adalah deret Konvergen maka batas - batas S adalah....
Jawab :
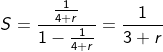
Konvergen : - 1 < r < 1
Jika r kita masukkan (-1) maka S = 1/2
Jika r kita masukkan (+1) maka S = 1/4
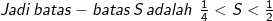
Tidak ada komentar:
Posting Komentar
Terima kasih atas kunjungan dan komentar ANDA